728x90
반응형
서포트 벡터 머신
- 서포트 벡터 머신은 벡터 공간에서 학습 데이터가 속한 2개의 그룹을 분류하는 선형 분리자를 찾는 기하학적 모델이다.
- 서포트 벡터 머신은 데이터를 분리하는 초평면 중에서 데이터들과 거리가 가장 먼 초평면을 선택하여 분리하는 지도 학습 기반의 이진 선형 분류 모델이다.
- 최대 마진을 가지는 비확률적 선형 판별 분석에 기초한 이진 분류기이다.
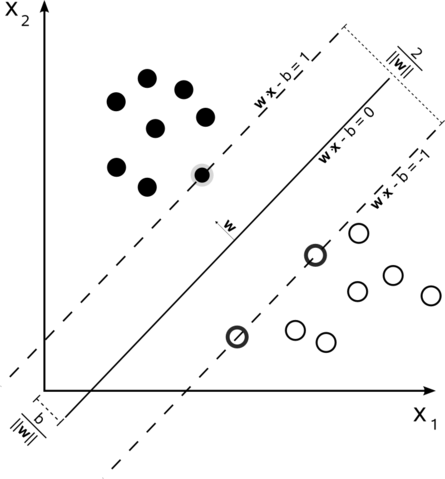
서포트 벡터 머신 특징
- SVM은 공간상에서 최적의 분리 초평면을 찾아서 분류 및 회귀를 수행한다,
- SVM은 변수 속성 간의 의존성은 고려하지 않으며 모든 속성을 활용하는 기법이다.
- SVM은 훈련 시간이 상대적으로 느리지만, 정확성이 뛰어나며 다른 방법보다 과대 적합의 가능성이 낮은 모델이다.
- 지도 학습 모델로 회귀 분석 및 분류(이항, 다항 모두 사용) 분석에 모두 사용한다.
서포트 벡터 머신의 구성요소
① 결정 경계(Decison Boundary)
- 데이터 분류의 기준이 되는 경계
② 초평면
- 데이터 분류를 위해서는 2개를 분리하는 결정영역이 있어야 하고, 이 결정영역을 결정짓기 위해서는 초평면 선택이 필요하다.
- 초평면은 데이터 임베딩 공간에서한 차원 낮은 부분 공간이다.
- 데이터가 n차원이라면 초평면은 (n-1)차원을 가지다.
③ 마진(Margin)
- 마진은 결정 경계와 서포트 벡터 사이의 거리를 의미한다.
- 결정 경계에서 서포트 벡터까지의 거리(즉, 여유 공간)
- 최적의 결정 경계를 구하기 위해서는 결정영역의 초평면을 둘러싸고 있는 마진을 최대화 시켜야한다.
- 모델 매개변수의 개수를 크게 줄여도 대상을 잘 분류할 수 있다는 장점이있다.
④ 서포트 벡터
- 학습 데이터 중에서 결정 경계와 가장 가까이에 있는 데이터들의 집합
⑤ 슬랙 변수
- 완벽한 분리가 불가능할 때 선형적으로 분류를 위해 허용된 오차를 위한 변수
- soft margin svm에서 사용
서포트 벡터 머신 종류
- SVM에는 하드 마진 SVM과 소프트 마신 SVM으로 나눌 수 있다.
① 하드 마진 SVM
- 마진의 안쪽이나 바깥쪽에 절대로 잘못 분류된 오 분류를 허용하지 않는 SVM
- 노이즈로 인하여 쵲거의 결정 경계를 잘못 구할 수도 있고, 못 찾을 경우도 발생할 수가 있음
②소프트 마진 SVM
- 마진의 안쪽이나 바깥쪽에 절대로 잘못 분류된 오 분류를 허용하는 SVM
- 하드 마진 SVM은 적용하기가 어려우므로어느 정도의 오류를 허용하는 소프트 마진 SVM을 주로 이용
서포트 벡터 머신 적용 기준
- 선형으로 분리가 가능한지 불가능한지에 따라 적용하는 방식이 다르다.
① 선형으로 분리 가능한 SVM
- 최적의 결정 경계(또는 초 평면)을 기준으로 1과 -1로 구분하여 분류 모형으로 사용한다.
② 선형으로 분리 불가능한 SVM
- 저차원 공간을 고차원 공간으로 매핑할 경우에 ㅂ라생하는 연산의 복잡성은 커널 트릭을 통하여 해결이 가능하다.
- 커널 트릭은 커널 함수(저차원에서 함수의 계산만으로 원하는 풀이가 가능한 함수)를 이용하여 고차원 공간으로 매핑 할 경우에 증가하는 연산량의 문제를 해결하는 기법
커널 함수의 종류
① 선형 커널
- 기본 유형의 커널이며, 1차원이고 다른 함수보다 빠르다.
- 텍스트 분류 문제에 주로 사용함
② 다항 커널 (Polynomial)
- 사용자가 지정한 차수의 다항식을 활용하는 커널이다.
- 선형 커널의 일반화된 공식이며, 효과성과 정확도 측면에서 효율이 적어 선호하지 않는다.
③ 가우시안 커널(Gaussian)
- 일반적으로 사용하는 커널이며, 데이터에 대한 사전 지식이 없는 경우 활용된다.
- 데이터에 대한 사전 지식이 없는 경우 적절하게 분리할 때 활용된다.
④ 가우시안 RBF 커널(Gaussian Radial Basis Function)
- 가장 많이 사용하는 커널이며, 비선형 데이터에 대한 사전 지식이 없는 경우 활용된다.
⑤ 시그모이드 커널(Sigmoid Kernel)
- 인공신경망에서 선호되는 커널로서 인공신경망의 다층 퍼셉트론 모델과 유사하다.
서포트 벡터 초매개변수 종류
- 서포트 벡터의 초매개변수는 C와 gamma가 있다.
① C
- C는 데이터 샘플들이 다른 클래스에 놓이는 것은 허용하는 정도를 결정한다.
- C는 traing data를 정확히 구분할지 아니면 decision boundary를 일반화할지를 결정
- C가 크면 training포인트를 정확히 구분, C가 작으면 smooth한 결정 경계를 그림
- 결정 경계는 C가 크면 더 굴곡지고 C가 작으면 직선에 가까움
② Gamma
- Gamma는 결정 경계의 곡률을 결정한다.
- Gamma가 크다면 reach가 좁고, Gamma가 작다면 reach가 멀다는 뜻임
- reach는 결정 경계의 굴곡에 영향을 주는 데이터 범위이다.
- Gamma가 크면 과대적합의 위험이 있고 너무 작으면 과소적합의 위험이 있다.
- 결정 경계는 Gamma가 크면 더 굴곡지고, Gamma가 작으면 직선에 가까워진다.
서포트 벡터 머신의 장단점
① 장점
- 서포트 벡터만을 이용해서 결정 경계를 생성하므로 데이터가 적을 때 효과적이다.
- 새로운 데이터가 입력되면 전체 데이터 포인트와의 거리를 계산하지 않고 서포트 벡터와의 거리만 계싼하면 되기 때문에 연산량 최소화
- 정확성이 뛰어나며, 커널 트릭을 활용하여 비선형 모델 분류 가능
- 다른 모형보다 과대 적합의 가능성이 낮고, 노이즈의 영향이 적다.
② 단점
- 데이터 전처리 과정이 중요하다.
- 데이터 세트의 크기가 클 경우 모델링에 많이 시간이 소요된다.
- 데이터가 많아질수록 최적화된 테스트를 위한 테스트 과정이 많아져서 다른 모형에 비해 속도가 느리다.
- 커널과 모델의 매개변수를 조절하기 위해 많은 테스트가 필요하다.
서포트 벡터 기출문제
Q. 서포트 벡터 머신에 대한 설명으로 옳지 않은 것은? [2회차]
① 다른 모형에 비해 속도가 빠르다.
② 다른 모형보다 과대적합에 강하다.
③ 비선형으로 분류되는 모형에도 사용할 수 있다.
④ 서포트 벡터가 여러 개일 수 있다.
더보기
① 다른 모형에 비해 속도가 빠르다.
Q. 서포트 벡터머신의 커널함수로 Radial Basis Function(RBF)을 사용할 때 가장 적절하지 않은 것은?
① 가우시안 커널이라고도 하며 하이퍼 파라미터로 C, gamma가 있다.
② 하이퍼 파라미터 gamma값이 커질수록 과적합 위험이 높아진다.
③ 사용자가 지정한 차수의 다항식을 활용하는 커널이다.
④ 고차항이 될수록 특성의 중요도는 감소한다,
더보기
③ 사용자가 지정한 차수의 다항식을 활용하는 커널이다.
728x90
반응형
'자격증 > 빅데이터분석기사' 카테고리의 다른 글
| 빅데이터분석기사 필기 - 불균형 데이터 처리 방법과 기출문제 (0) | 2022.10.01 |
|---|---|
| [빅데이터분석기사 필기] 변수 변환 방법과 기출문제 (0) | 2022.10.01 |
| [빅데이터분석기사 필기] 2021년 2회차 기출문제 (2) | 2022.09.30 |
| [빅데이터분석기사 필기] 하둡 에코시스템의 다양한 기술과 기출문제 (1) | 2022.09.30 |
| [빅데이터분석기사 필기] 데이터 저장기술 종류와 기출문제 (0) | 2022.09.29 |