728x90
반응형

그래프(G)는 정점(V)과 간선(E)으로 이루어져 있음
그래프의 종류
-무방향 그래프: 간선에 방향성이 없음
-방향성 그래프: 간선에 방향성이 있음
-가중치그래프: 간선에 가중치가 부여된 그래프
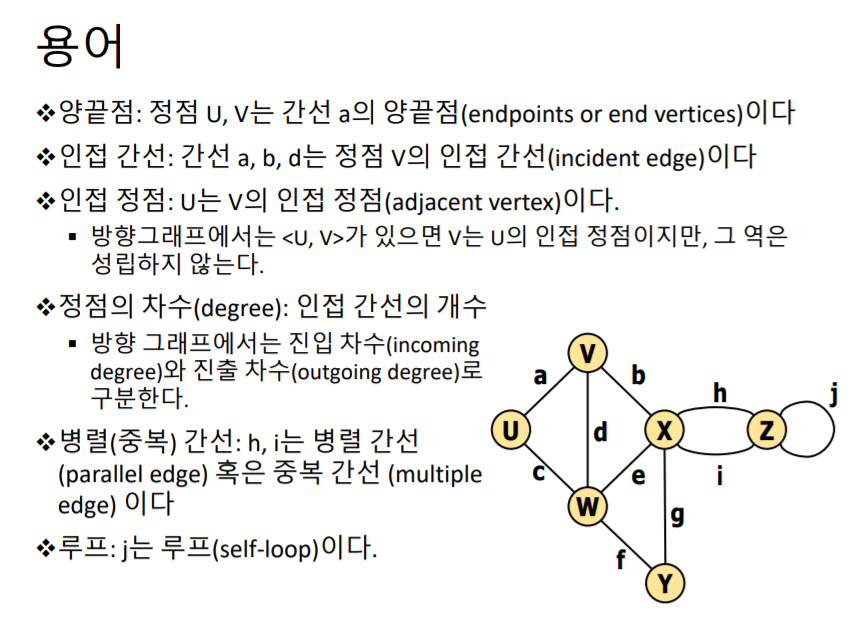
병렬 간선: X -> Z의 간선이 h,i 두개가 복수로 존개가능함
루프: 출발지 정점과 목적지 정점이 같은경우 ex) edge j

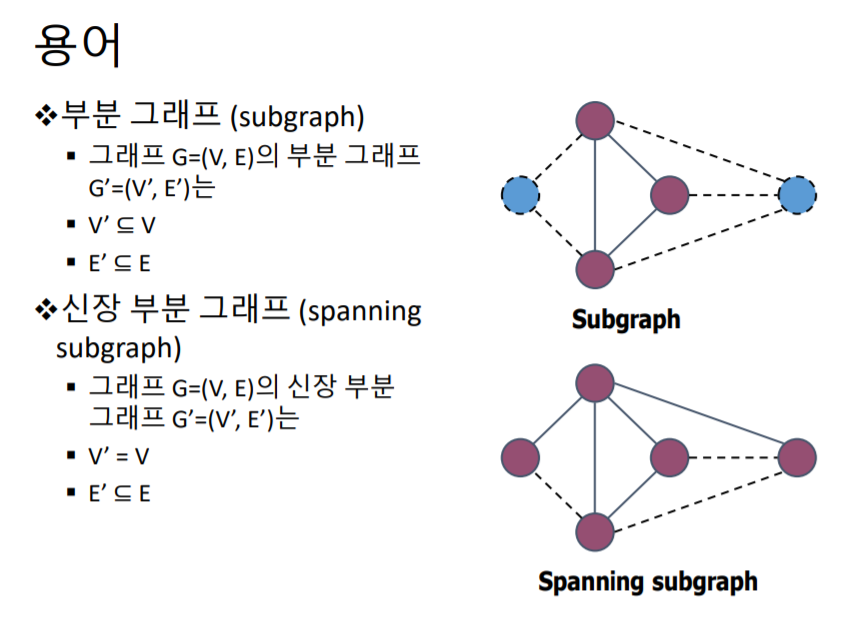
그래프G에서 점선을 다 지우면 G'인 그림임
부분 그래프: G'은 그래프G의 일부분임 V-V'을 잇는 E는 존재할 수없다.
신장부분그래프: 그래프 G'은 그래프G의 일부분인데 G의 모든 정점을 가지있음

연결 그래프: 모든 정점 간에 경로가 존재

트리는 연결그래프이고 Forest는 연결되지 않은 그래프임

파이썬으로 그래프 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
|
class Graph:
class Vertex:
def __init__(self, x):
self._element = x
def element(self):
return self._element
def __str__(self):
return str(self._element)
def __repr__(self):
return str(self._element)
class Edge:
def __init__(self, u, v, x):
self._source = u
self._destination = v
self._element = x
def element(self):
return self._element
def endpoints(self):
return self._source, self._destination
def opposite(self, p):
if p is self._source:
return self._destination
elif p is self._destination:
return self._source
else:
raise ValueError(f"{p} is not incident to {self}")
def __str__(self):
return f"({self._source}, {self._destination}, {self._element})"
def __repr__(self):
return f"({self._source}, {self._destination}, {self._element})"
def __init__(self, directed=False):
self._outgoing = {} # use dict instead of list
self._incoming = {} if directed else self._outgoing
def __str__(self):
return f"G=(V, E) with V={[str(v) for v in self.vertices()]}:{self.vertex_count()}, E={[str(e) for e in self.edges()]}:{self.edge_count()}"
def is_directed(self):
return self._outgoing is not self._incoming
def vertex_count(self):
"""Return the number of vertices in the graph"""
return len(self._outgoing)
def vertices(self):
"""Return the iterator of all the vertices in the graph"""
return self._outgoing.keys()
def edge_count(self):
"""return the number of edges in the graph"""
count = sum(len(self._outgoing[v]) for v in self._outgoing)
return count if self.is_directed() else count // 2
def edges(self):
"""Return the iterator of all the edges in the graph"""
result = set() # for remove duplication in case of undirected graph
for edge_map in self._outgoing.values():
result.update(edge_map.values()) # update edges
return result
def _validate_vertex(self, v):
if not isinstance(v, self.Vertex):
raise TypeError(f"{v} is not an instance of Vertex")
if v not in self._outgoing:
raise ValueError(f"{v} is not a vertex in this graph.")
def get_edge(self, u, v):
self._validate_vertex(u)
self._validate_vertex(v)
return self._outgoing[u].get(v) # return None if v is not adjacent to u
def incident_edges(self, v, outgoing=True):
self._validate_vertex(v)
adj = self._outgoing if outgoing else self._incoming
for edge in adj[v].values():
yield edge
def degree(self, v, outgoing=True):
self._validate_vertex(v)
adj = self._outgoing if outgoing else self._incoming
return len(adj[v])
def insert_vertex(self, x=None):
v = self.Vertex(x)
self._outgoing[v] = {}
if self.is_directed():
self._incoming[v] = {}
return v
def insert_edge(self, u, v, x=None):
if self.get_edge(u, v):
raise ValueError(f"{u} and {v} are already adjacent in this graph.")
e = self.Edge(u, v, x)
self._outgoing[u][v] = e
self._incoming[v][u] = e
return e
if "__main__":
G = Graph(directed=True)
v = ['u', 'v', 'w', 'z'] #정점
verts = {}
for i in range(4):
verts[i] = G.insert_vertex(v[i])
G.insert_edge(verts[0], verts[1], 'e')
G.insert_edge(verts[0], verts[2], 'g')
G.insert_edge(verts[1], verts[2], 'f')
G.insert_edge(verts[2], verts[3], 'h')
print(G)
|
cs |

위의 그림으로 테스트 한 결과
G=(V, E) with V=['u', 'v', 'w', 'z']:4, E=['(u, w, g)', '(u, v, e)', '(v, w, f)', '(w, z, h)']:4
4개의 정점을 가지고 있고 4개의 간선을 가지고 있는 그래프를 생성함
728x90
반응형
'자료구조' 카테고리의 다른 글
| [파이썬 자료구조] Partition or Disjoint Set (0) | 2020.06.20 |
|---|---|
| [파이썬 자료구조] Kruskal 알고리즘 (0) | 2020.06.20 |
| [파이썬 자료구조] 방향그래프 (Directed Graph) (0) | 2020.06.17 |
| [파이썬 자료구조] 너비우선탐색(BFS, Breadth-First Search) (0) | 2020.06.16 |
| [파이썬 자료구조] 깊이 우선 탐색 (DFS, depth first traversal) (0) | 2020.06.16 |